背包问题
一、背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
** 朴素版解法:二维空间解法
每件物品只能选一次,对于每种物品,我们有两种选择 **
**1. 不选 -> dp[i][j]=dp[i-1][j]
等于选前 i - 1 个物品,空间为 j 情况下的最优解
2. 选 -> dp[i][j]=dp[i-1][j-v[i]]+w[i]
如果选的话,前 i - 1 个物品的体积最多为 j -v[i]**
在这两种情况中取较大值即可,即为当前情况的最优解,我们的每一步都是从上一步的最优解转移过来,所以可以保证最后的结果一定是最优解
#include<iostream>
using namespace std;
#define N 1005
int dp[N][N]; //dp[i][j]表示前i个物品,背包容量是j的情况下的最大价值。
int w[N];
int v[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d%d",&v[i],&w[i]);
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=v[i])
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
}
}
cout<<dp[n][m]<<endl;
return 0;
}
解法二:滚动数组优化:(实际上只需要一个数组)
** 状态转移每次只与上一层有关,所以用一个一维数组就可以
转移方程:dp[i]=max(dp[i],dp[i-v[i]]+w[i])**
其实就相当于二维中的 dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i])
所以第二层循环需要从大到小循环,因为若是继续从小到大循环,后面算的时候,用的是这一层已经算过的数据,就变成 dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]) ,(这正好是完全背包一维的解法,每个物品可以选无限次)而从大到小算的话一定用的是上一层的状态
#include<iostream>
using namespace std;
#define N 1005
int dp[N];
int main()
{
int n,m,v,w;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v>>w;
for(int j=m;j>=v;j--)
{
dp[j]=max(dp[j],dp[j-v]+w);
}
}
cout<<dp[m]<<endl;
return 0;
}
** 注:这时的 dp[i]表示空间 <= i 的最大价值,所以最后直接输出 dp[m]即可,这与初始化有关,因为 dp 数组在主函数外定义,初始值均为 0,所以如果存在一个 k <m 使得空间最大为 k 的情况下 dp[k]有最大价值,那么 dp[m]一定可以从 k 这个状态转移过来—即 dp[m]一定是最大值。
若题目要求装满背包,即将物品恰装入一个容量为 m 的背包中,只需要将初始化条件改一改即可,---- 将 dp 数组初始化为负无穷,dp[0]=0,即可确保状态一定是从 0 转移过来的。**
二、完全背包问题
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
10
** 朴素版解法:二维空间解法
也是两种选择,选或不选,只不过每个物品可以选无限次,在 01 的基础上把
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i])
改为
dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i])即可 **
#include<iostream>
using namespace std;
#define N 1005
int dp[N][N];
int w[N];
int v[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d%d",&v[i],&w[i]);
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=v[i])
dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);
}
}
cout<<dp[n][m]<<endl;
return 0;
}
** 优化空间版解法:
转移方程为 dp[j]=max(dp[j],dp[j-v[i]]+w[i])
第二层从小到大循环,原因参见 01 的一维 **
#include<iostream>
using namespace std;
#define N 1005
int dp[N];
int main()
{
int n,m,w,v;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v>>w;
for(int j=v;j<=m;j++)
{
dp[j]=max(dp[j],dp[j-v]+w);
}
}
cout<<dp[m]<<endl;
return 0;
}
三、多重背包问题
题目 1:o(n^3)做法
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<vi,wi,si≤100
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
** 思路:是 01 背包的延伸,就不说二维做法了,跟上面差不多。直接贴一维做法。
01 背包是选或不选 :
dp[j]=max(dp[j],dp[j-v[i]]+w[i])
多重背包是选 0 个,1 个,2 个…s[i]个
即 dp[j]=max(dp[j],dp[j - v[i] k]+w[i] k)
k=1,2,3,…s[i]
那么再加一层循环表示选多少个就可以了
因为是 01 背包的扩展,所以第二层循环应从大到小循环 **
#include<iostream>
using namespace std;
#define N 105
int w[N];
int v[N];
int s[N];
int dp[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d%d%d",&v[i],&w[i],&s[i]);
for(int i=1;i<=n;i++)
{
for(int j=m;j>=v[i];j--)
{
for(int k=1;k<=s[i] && j>=k*v[i];k++)
dp[j]=max(dp[j],dp[j-k*v[i]]+w[i]*k);
}
}
cout<<dp[m]<<endl;
return 0;
}
方法 2:二进制优化做法
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 ii 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V≤2000
0<vi,wi,si≤2000
提示:
本题考查多重背包的二进制优化方法。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
思路:这道题的数据范围如果用三层循环的话是达到了 1e9,所以必须优化它。其实可以把它转化为一个 01 背包的问题。每个物品有 s 件,我们可以把它差分成 s 份,每份物品当做不同的个体,即只能选一次,这就转化为了 01 背包物品,但是这样的话,物品个数变成了 1000*2000=2e6,再循环一层空间的话,还是 1e9 的复杂度。
** 那么继续优化,一个物品的数量是 s 的话,只要把 s 拆分成一些数字,使它们能够表示出 1 - s 中任意一个数字,就可以,没必要把它拆成 s 个 1。
那么这样的数字最少需要多少个呢?最少需要 log(s)个,向上取整。
比如 7,它最少需要 3 个数字来表示:
即 1(2^0=1 ), 2(2^1=2), 4(2^2=4)。
原因:每个数字有 2 种可能选或不选,那么可以表示的不同数字个数就是 2 2 2 = 8。但是还需要注意一个问题,就是有些数字可能能够表示出来一些大于 s 的数字,但是这件物品最多只有 s 件,那么就需要特殊处理一下最后一个数。
比如 10,若用 1,2, 4, 8 表示,可能会表示出来大于 10 的数字,例如:4+8=12。那么如果最后一个数字加上前面数的总和会大于 s,就将它替换为剩下的物品个数,即将 8 替换为 3,这时正好能表示出 1 - s 所有的数,-> 1, 2,4 可以表示 7 以内的所有数,这些数加上 3 就可以表示 10 以内的所有数啦。
注:如果拆分成 log(s)个的话,时间复杂度就变为 1000 log(2000) 2000 = 2e7,是可以通过的~**
#include<iostream>
#include<vector>
using namespace std;
#define N 2005
int dp[N];
struct node
{
int v,w;
};
vector<node> goods; //因为不确定一共能拆分出来多少份物品,所以用容器存储
int main()
{
int n,m,s,v,w;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>v>>w>>s;
for(int j=1;j<=s;j*=2)
{
goods.push_back({v*j,w*j});
s-=j;
}
if(s) //最后需要特判的数
goods.push_back({v*s,w*s});
}
for(int i=0;i<goods.size();i++)
{
for(int j=m;j>=goods[i].v;j--)
{
dp[j]=max(dp[j],dp[j-goods[i].v]+goods[i].w);
}
}
cout<<dp[m]<<endl;
return 0;
}
题目 3:多重背包终极版… Acwing 06
题目跟上面一样,但是数据范围如下 
用的是单调队列优化,效果是把那层 log(s)去掉,变成 n * v 的复杂度。本人小菜鸟,看了好几遍没看懂咋做的 T.T。感兴趣的童鞋们可以去点我最下面贴的视频链接,去看大佬的讲解。
四、混合背包问题
有 N 种物品和一个容量是 V 的背包。
物品一共有三类:
第一类物品只能用 1 次(01 背包);
第二类物品可以用无限次(完全背包);
第三类物品最多只能用 si 次(多重背包);
每种体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
si=−1 表示第 i 种物品只能用 1 次;
si=0 表示第 i 种物品可以用无限次;
si>0 表示第 i 种物品可以使用 si 次;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
−1≤si≤1000−1
输入样例
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
输出样例:
8
思路:是一个前三种背包问题的综合,如果明白了前面的,就很简单了,只需要判断一下类型,如果是多重背包,将它转换为 01 背包插入数组当中,然后按着不同类型的处理方式去遍历空间大小即可。
#include<iostream>
#include<vector>
using namespace std;
#define N 1005
int dp[N];
struct node
{
int v,w,flag;
};
int main()
{
vector<node> goods;
int n,m,v,w,s;
cin>>n>>m;
for(int i=0;i<n;i++)
{
cin>>v>>w>>s;
if(s>0) //如果是多重背包,二进制优化,将其转换为01背包
{
for(int j=1;j<=s;j*=2)
{
goods.push_back({v*j,w*j,-1});
s-=j;
}
if(s)
goods.push_back({v*s,w*s,-1});
}
else
goods.push_back({v,w,s});
}
for(int i=0;i<goods.size();i++)
{
if(goods[i].flag==0)
{
for(int j=goods[i].v;j<=m;j++) //如果是完全背包,从小到大枚举
dp[j]=max(dp[j],dp[j-goods[i].v]+goods[i].w);
continue;
}
for(int j=m;j>=goods[i].v;j--) //如果是01背包,从大到小枚举
{
dp[j]=max(dp[j],dp[j-goods[i].v]+goods[i].w);
}
}
cout<<dp[m]<<endl;
return 0;
}
五、二维费用的背包问题
有 N 件物品和一个容量是 V 的背包,背包能承受的最大重量是 M。
每件物品只能用一次。体积是 vi,重量是 mi,价值是 wi。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V, M,用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 N 行,每行三个整数 vi,mi,wi,用空格隔开,分别表示第 i 件物品的体积、重量和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V,M≤100
0<vi,mi≤100
0<wi≤1000
输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例:
8
思路:这个题也很简单,就是在 01 背包的基础上加了一维重量,枚举的时候多一层循环就行了。因为是 01 背包的变形,所以重量和体积枚举的时候都从大到小枚举。
#include<iostream>
using namespace std;
#define N 1005
int dp[N][N];
int main()
{
int n,V,M,v,w,m;
cin>>n>>V>>M;
for(int i=0;i<n;i++)
{
cin>>v>>m>>w;
for(int j=V;j>=v;j--)
{
for(int k=M;k>=m;k--)
dp[j][k]=max(dp[j][k],dp[j-v][k-m]+w);
}
}
cout<<dp[V][M]<<endl;
return 0;
}
六、分组背包问题
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
每组数据第一行有一个整数 Si,表示第 i 个物品组的物品数量;
每组数据接下来有 Si 行,每行有两个整数 vij,wij,用空格隔开,分别表示第 i 个物品组的第 j 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<Si≤100
0<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例:
8
思路:和多重背包有一些类似,多重背包是每个物品有 si 件,可以选 0,1,2…si 件。而分组背包是不选,选第 1 个,或第 2 个或第 3 个…或第 si 个,都有 si+ 1 种决策方式,即使用三层循环即可解决。没有优化方式。
#include<iostream>
#include<vector>
using namespace std;
#define N 105
int dp[N];
int v[N];
int w[N];
int main()
{
int n,m,s;
cin>>n>>m;
for(int i=0;i<n;i++)
{
cin>>s;
for(int k=0;k<s;k++)
cin>>v[k]>>w[k];
for(int j=m;j>=0;j--)
for(int k=0;k<s;k++)
if(j>=v[k])
dp[j]=max(dp[j],dp[j-v[k]]+w[k]);
}
cout<<dp[m]<<endl;
return 0;
}
七、有依赖的背包问题
有 NN 个物品和一个容量是 VV 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示: 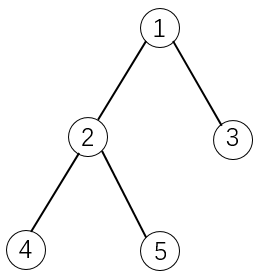
如果选择物品 5,则必须选择物品 1 和 2。这是因为 2 是 5 的父节点,1 是 2 的父节点。
每件物品的编号是 ii,体积是 vivi,价值是 wiwi,依赖的父节点编号是 pipi。物品的下标范围是 1…N1…N。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,VN,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 NN 行数据,每行数据表示一个物品。
第 ii 行有三个整数 vi,wi,pivi,wi,pi,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1pi=−1,表示根节点。 数据保证所有物品构成一棵树。
输出格式
输出一个整数,表示最大价值。
数据范围
1≤N,V≤1001≤N,V≤100
1≤vi,wi≤1001≤vi,wi≤100
父节点编号范围:
内部结点:1≤pi≤N1≤pi≤N;
根节点 pi=−1pi=−1;
输入样例
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出样例:
11
** 思路:其实有依赖的背包问题和树形 dp 很类似,它把树形 dp 和分组背包结合到了一起。
选一个物品必须要选择它的父节点,那么反过来,父节点选择子节点,一定会选择价值最大的那一分支。那么就可以先递归算出子树的每一个体积对应的最大价值,然后进行分组背包,求出最大值即可。**
需要注意的是,我们选择了子节点,就必须选择当前节点,那么最后需要把父节点的位置空出来。(把所有已算完的体积更新一下,在里面加上父节点这一物品)
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N =1005;
int e[N],w[N],v[N],ne[N],h[N],idx;
int dp[105][105];
int n,m;
void init()
{
memset(h,-1,sizeof h);
idx=0;
}
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int x)
{
for(int i=h[x];i!=-1;i=ne[i])
{
int son=e[i];
dfs(son);
for(int j=m;j>=0;j--)
{
for(int k=0;k<=j;k++)
dp[x][j]=max(dp[x][j],dp[x][j-k]+dp[son][k]);
}
}
for(int i=m;i>=0;i--)
if(i>=v[x])
dp[x][i]=dp[x][i-v[x]]+w[x];
else //注意,父节点不选的话,子节点一个都不能选
dp[x][i]=0;
}
int main()
{
init();
int root;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
int fa;
scanf("%d%d%d",&v[i],&w[i],&fa);
if(fa==-1)
root=i;
else
add(fa,i);
}
dfs(root);
cout<<dp[root][m]<<endl;
return 0;
}
八、背包问题求方案数
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 10^9+7 的结果。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 ii 件物品的体积和价值。
输出格式
输出一个整数,表示 方案数 模 10^9+ 7 的结果。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例:
2
思路:在原来 01 背包的基础上加一个表示方案数的数组即可。注意初始化,如果只把 num[0]赋值成 1,那么需要把对应的 01 背包转化为体积恰好是 j 的情况下的最大价值。最后找出最大价值,将此价值对应的所有体积的方案数加上即可。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define inf 0x3f3f3f3f
const int mod=1e9+7;
const int N =1005;
int dp[N],num[N],v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d%d",&v[i],&w[i]);
memset(dp,-inf,sizeof dp);
dp[0]=0;num[0]=1;
int maxw=0;
for(int i=1;i<=n;i++)
{
for(int j=m;j>=v[i];j--)
{
if(dp[j-v[i]]+w[i]>dp[j])
{
dp[j]=dp[j-v[i]]+w[i];
num[j]=num[j-v[i]];
}
else if(dp[j-v[i]]+w[i]==dp[j])
num[j]=(num[j]+num[j-v[i]])%mod;
}
}
for(int i=0;i<=m;i++)
maxw=max(maxw,dp[i]);
int ans=0;
for(int i=0;i<=m;i++)
if(dp[i]==maxw)
ans=(ans+num[i])%mod;
cout<<ans<<endl;
return 0;
}
九、背包问题求具体方案
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是 1…N。
输入格式
第一行两个整数,N,V 用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 1…N。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例:
1 4
思路:因为方案可能有很多种,题目要求输出字典序最小的,那么就倒着枚举物品种类,贪心思想,确保序号小的能优先选择。最后输出一下可行的转移路径就行了。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N =1005;
int dp[N][N],v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d%d",&v[i],&w[i]);
for(int i=n;i>=1;i--)
{
for(int j=m;j>=0;j--)
{
dp[i][j]=dp[i+1][j];
if(j>=v[i])
dp[i][j]=max(dp[i][j],dp[i+1][j-v[i]]+w[i]);
}
}
int val=m;
for(int i=1;i<=n;i++)
{
if(val-v[i]>=0&&dp[i][val]==dp[i+1][val-v[i]]+w[i])
{
cout<<i<<" ";
val-=v[i];
}
}
return 0;
}